A kto wie, co dzisiaj jest za dzień? Pytanie za 100 pkt. jako że nawet Google nie wiedziało (i obchodziło dzisiaj urodziny jakiegoś Japończyka czy Chińczyka), choć nie zapomina Wikipedia.
Dzisiaj jest Dzień liczby π!
stąd
π! Kolejna z rzeczy, z którą, niczym z 29 lutego, ludzie męczyli się od starożytności! Bo wiecie - dawno dawno temu, w Grecji bodajże, mieli bzika na punkcie proporcji, równowagi i wdzięku sprowadzania wszystkiego do liczb całkowitych. A tu nagle pojawia się liczba, która bierze się z Bogu ducha winnego koła, znaczy: ze stosunku jego obwodu do średnicy i, pomimo że jest ładna i zawsze niezmienna, zwyczajnie nie da się, no NIE DA SIĘ przerobić tego na ułamek zwykły! Matematycy starożytności zgłupieli - przecież zgodnie z ich normami taki wybryk nie był nawet liczbą!
No i się zaczęło...
Generalnie problem był, hmm, dość problemowy. Jak donosi Wikipedia na początku się przemilczało i π miało mieć około 3 czy 3,12. Jak opowiadają tutaj jedną z pierwszych osób, która odważyła się jakoś ugryźć ten temat, był Archimedes, który przybliżył je jako 22/7, czyli, skracając, mniej więcej 3,142857.
Potem był doszedł Klaudiusz Ptolemeusz, który wynikiem 3,1416 przebił go o jedną tysiączną. Potem...
Ale jak oni to robili? No wyobraźcie to sobie - macie kółko i obwód, do tego linijkę i sznurek. I co? Przecież z mierzenia obwodu w ten sposób nie wyjdzie Wam 10,39898203591190204542899057614986223, tylko pewnie jakieś 10,5 ;) I jeszcze weź toto podziel... A starożytni naprawdę potrafili! I oni nie mieli komputerów, o czym myślenie automatycznie nam się wyłącza. Mogę jedynie poinformować, że kiedy dzisiejsi naukowcy tłumaczą nam, że tacy Babilończycy obliczyli coś tam i wiele innych rzeczy z dokładnością do dwusetnego miejsca po przecinku, to znaczy, że pisali po prostu coś w stylu 239/1636.
Czyli część problemu mieli z głowy. Ale jednak ten nieszczęsny obwód musieli znaleźć! I, pomijając początki, wszyscy na wszystkich kontynentach, robili to zgodnie i celnie, z uwagą, cierpliwością i szacunkiem, z każdym rokiem dokładniej i z większą ciekawością. I chyba nawet szybciej niż by nam się zdawało, skoro nawet piramidę Cheopsa robili pod linijkę dla tej liczby. A potem toooo... już nawet nie będę języka strzępić, skoro Wikipedia może lepiej. Dowody niewymierności, wzory do obliczania go i za jego pomocą, nazewnictwo...
Zwrócę uwagę tylko na jeden jedyny wzór, na który, podobnie jak każdy matematyk i niektórzy superbohaterowie, napatrzeć się nie mogę:
...który wymyślił pan Leonhard Euler, który pieszczotliwie zwany jest najpiękniejszych wzorem matematyki i o którym, jeśli jeszcze komuś mało, jest więcej tutaj.
Tym, co znalazłam na tamtej stronie, a wzbudziło mój szczególny podziw, było coś, co określili jako Trójwymiarowa ilustracja wzoru Eulera:
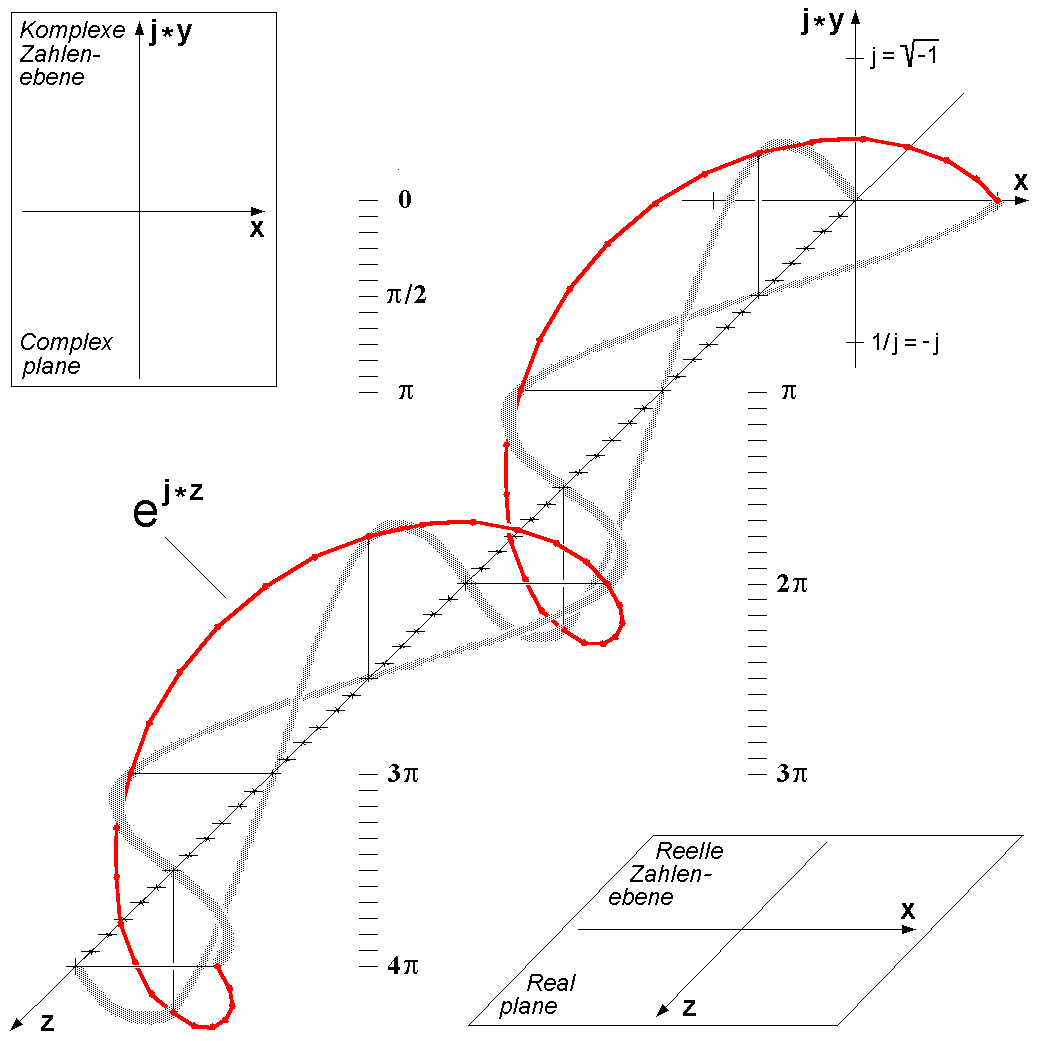
(Tutaj już nie zachowałam się co prawda jak na prawdziwego matematyka przystało, bo patrząc na ten wykres odruchowo poczułam się, jakbym wysiadła właśnie z kolejki o takim kształcie, ale mniejsza.)
Liczby zespolone! Geometria! Fizyka! Tak, tak, moi drodzy! π było niczym nasionka od maliny - właziło wszędzie! Nic dziwnego, że poodkrywano tysiące sposobów na to, żeby w domowym zaciszu każda gospodyni domowa mogła po cichu oddać się przyjemności samodzielnego poznawania kolejnych cyferek (to jest podobno jedna z tych rzeczy, którą każda gospodyni domowa robi, ale nie ma odwagi się przyznać). Parę sympatycznych sposobów podają tutaj, w Wikipedii jeszcze więcej (choć przyznać trzeba, że już nieco mniej sympatycznych). Jednakże...
Bardzo się zdziwiłam, ponieważ nie ma na żadnej z tych stron słowa o pewnej uroczo kontrowersyjnej metodzie liczenia, o której kiedyś całkiem przypadkiem dowiedziałam się z ostatnich stron pewnej książki o statystyce (Monstrualna erudycja nawiasem mówiąc, zalecam ;) ). Do dzisiaj dnia odsuwałam myśl o tym, czy znajdę informacje o niej w Internecie, ponieważ moja superbohaterska pamięć lubi płatać figle, a nie chciałam napleść bzdur. Zaczęłam szukać i... JEST! Jak tylko zobaczyłam w skrócie wspomnienie o metod Monte Carlo, w której się najpierw strzela, potem liczy, od razu wiedziałam!
Otóż pewien pan Georges-Louis Leclerc Buffon, czyli w skrócie po prostu Buffon (
), który zauważył, że jak weźmie paczkę igieł, narysuje linie w odstępach równych długości tych igieł i rzuci igły na te linie, to stosunek liczby wszystkich igieł do tych, które upadły na linie będzie bliski π/2 !
gdzie:
n to wszystkie igły;
R to liczba upadniętych na kreskę.
Bliski π/2 i tym bliższy, im więcej igieł będzie nam się chciało zbierać z podłogi!
Problem igły Buffona został jednak na Wikipedii rozciągnięty na zależności od długości igieł i samej zależności od π nie widać aż tak bardzo, więc dla pewności podrzucam jeszcze jedną stronę (Zadanie nr 4), która co prawda wzór układa nieco w inny sposób, ale za to dysponuje ładnym obrazkiem:
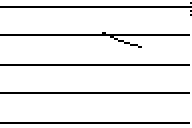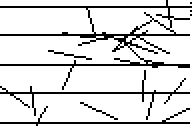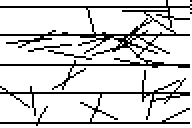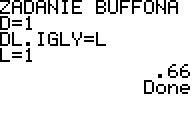
No. I już widzę, jak jutro w sklepach kolejki za szpilkopodobnymi rzeczami będą ;p
Google nic nie mówiło, a ja wiedziałam - skąd? Otóż kiedy zaczynałam liceum dni na cześć liczby π były urządzane w mojej szkole. Robiło się rysunki, pisało wierszyki... Najlepiej jednak wspominam konkurs na szukanie swojej daty urodzenia w długich mrocznych ciągach tej nieskończonej liczby. No wiecie: ktoś jest z 15 października 1999, to szuka 15101999. Albo 19991510. Albo jeszcze inaczej. W sumie za 151099 też chyba nie nabijali na pal :) Nikt się też nie czepiał nawet takich szczęściarzy jak ja, którzy mieli jednocyfrowe numery miesięcy i dni, przez co szukali np. nie tylko 01021999, ale też 121999, 199912, 2199, itp. ...
Czekam na propozycje czytelników
Jeśli chodzi o utwory literackie, to niczego wartego uwagi z czasów liceum nie pamiętam. Każdy wstawiłby w takiej chwili dzieło pani Szymborskiej pod tytułem Liczba pi, jednak ja nie uważam go za udany. Mógłby być lepszy, a jest taki nadmuchany. Tym co ja napiszę, będzie coś, o czym kiedyś na jednych z zajęć Javy wspomniał nam pan dr Wercinski Tomasz, a co (jeszcze bardziej kiedyś) zdarzyło mu się przeczytać:
Pewnego razu pani na zajęciach z matematyki opowiadała o obliczeniach związanych z kołem i w ramach zadania domowego poleciła uczniom jak najdokładniejsze obliczenie wartości liczby π Następnego dnia zaczęły się dziać rzeczy niezwykłe. Kolejni rodzice zaczęli zgłaszać się z przeprosinami, że nie potrafią jak należy pomóc dziecku w lekcjach, bo po zmierzeniu koła jak najdokładniejszymi sposobami i dokonaniu dzielenia wychodzi im... równo 3. Za pierwszym razem nauczycielka się śmiała, jednak zgłaszali się kolejni rodzice - skruszeni tłumaczyli, że nie wiedzą, co robią źle, jednak musieli przy dziecku bezradnie skrobać się po głowach, bo nie wychodziło im nawet w przybliżeniu legendarne 3,14.
Szybko po wydarzeniach w szkole informacje o dziwnych problemach z obliczeniami zaczęły się pojawiać także w wiadomościach telewizyjnych, w radiu i wszędzie, na całym świecie. Nagle nikomu już w budowie, inżynierii i tak dalej nie zgadzało się, żeby π miało 3,1415 i więcej! Nastąpiła panika i wszechogarniające zdziwienie. Koło nadal było kołem, jednak stosunek długości okręgu do środnicy wynosił dokładnie 3 i żadna ze starych regół nie nadawała się do stosowania! Wszystkie programy komputerowe, wypracowane podejścia, wzory okazały się omylne i bezwartościowe...
Centralnie, albo Doctor coś tam musiał zrypać albo Chuck Norris nie tak trzasnął drzwiami O.o
Na koniec coś ode mnie. Wspominałam, że były konkursy rysownicze, w takim razie przedstawiam, jaką wizję narysowałam w 2005 roku:
:)
Nie znam żadnej piosenki, która choć wydawałaby się mieć coś wspólnego z liczbą π, więc zapodam to, co mi się dzisiaj bardzo nadało. Tak bardzo, że aż wyszukałam w Internecie po słowach, co to za piosenka, którą dotychczas miałam zapisaną tylko jako no_name:
Ale oczywiście, jeśli ktoś chce, żeby było bardziej nastrojowo, można sobie wyobrazić, że ten pan śpiewa o π.
Brak komentarzy:
Prześlij komentarz